Llaves de cortante y pernos en placas de anclaje: Reparto del cortante

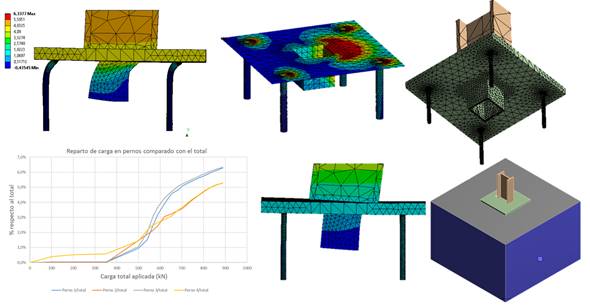
Las placas de anclaje, cuando están sometidas a fuerzas importantes de cortante, se les suele soldar en su parte inferior un perfil en I, rectangular o tubular, también conocido como llave de cortante. El objetivo de esta llave de cortante es, como parece lógico, resistir el cortante, descargando así los pernos que ya estarán trabajando a tracción. Sin embargo, surge la duda de si la llave de cortante va a resistir todo el cortante dado que es más rígido que los pernos, o si por el contrario, los pernos resistirán una parte de este cortante. En muchos cálculos se tiende a hacer la hipótesis de que el cortante se trasmite en su totalidad a través de la llave de cortante, trabajando así los pernos solo a tracción. El objetivo de este artículo es estudiar si esta hipótesis es correcta.

Notamos en el EC-2 una ausencia importante en cuanto a llaves de cortante en general, y una ausencia completa en cuanto al tema tratado en este artículo. No se pronuncia nada sobre cómo tratar la trasmisión de cortante cuando disponemos de llaves de cortante. Sin embargo, el código americano, ACI 318-19, sí que entra más en detalle en este tema. La ACI 318-19 dice en su punto §17.11.1.1.3:

§17.11.1.1.3 – For anchors welded to the attachment base plate, tension and shear requirements of 17.8 shall include a portion of the total shear of the anchor

Y explica, en su versión con comentarios, lo siguiente sobre este punto §17.11.1.1.3:

§R17.11.1.1.3 – Although neglected in the bearing strength evaluation in 17.11.2, welded anchors resist a portion of the shear load because they displace the same as the shear lug. The portion of the applied shear, Vu, that each anchor carries, Vuad, is given by

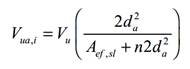
Donde n es el número de pernos y Aef,sl es el área de la llave de cortante que va a apoyar contra el hormigón y que definimos más adelante.

Esto nos quiere decir que efectivamente tenemos que tener en cuenta que una cierta parte de nuestro cortante se va a transmitir a través de los pernos, invalidando la hipótesis de que la llave de cortante resiste todo el cortante.

Vamos a comprobar, mediante un modelo de cálculo de elementos finitos (MEF), la veracidad de la fórmula anterior. Para ello, hemos modelizado una placa de anclaje de 35mm de espesor con 4 pernos M16 de 200mm de longitud. Lleva soldado una llave de cortante tubular cuadrada de 110x115x7.5 (mm – Alto x Ancho x Espesor). Sobre ella se ha soldado un perfil en I sobre el que aplicaremos la carga de cortante. Sus dimensiones no tienen un peso importante en el cálculo, tan solo aseguramos que sea coherente con el tamaño de los otros elementos de la placa (210x120 con un alma de 14mm y un ala de 17mm) para que reparta los esfuerzos en una zona representativa de la placa.

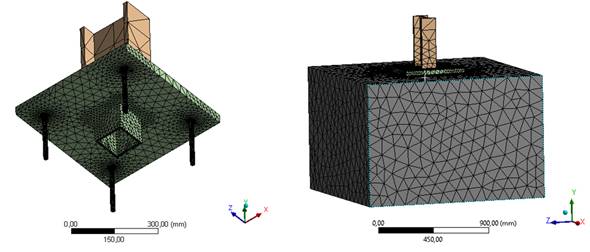
Figura 1. Modelo de elementos finitos (MEF) - Mallado 

Se han modelado apoyos verticales (dirección Y) en cabeza del perfil en I para simular el efecto del resto de la estructura y también apoyos verticales en la parte inferior de los anclajes para simular la cabeza de anclaje del perno que bloquea los desplazamientos verticales. La siguiente imagen nos muestra estas condiciones de contorno:

Figura 2. Condiciones de contorno – Apoyo vertical

Los cuatro lados del bloque de hormigón están bloqueados para representar la continuidad de la estructura donde está anclada nuestra placa tal como se muestra en la siguiente imagen:

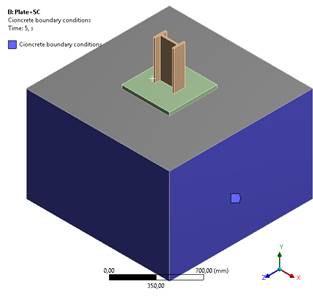
Figura 3. Condiciones de contorno – Hormigón

La interacción entre la placa y el hormigón se ha modelado mediante contactos sin deslizamiento, es decir que permiten solo contacto en compresión y que no tiene resistencia tangencial (frotamiento). La siguiente imagen nos muestra los contactos usados:

Figura 4. Condiciones de contorno – Contactos entre placa y hormigón

Aplicamos una fuerza horizontal creciente en el ala del perfil. En función de esta fuerza vamos a obtener la reacción en la llave de cortante y en cada uno de los pernos para poder compararla con la obtenida aplicando la fórmula de la ACI 318-19.

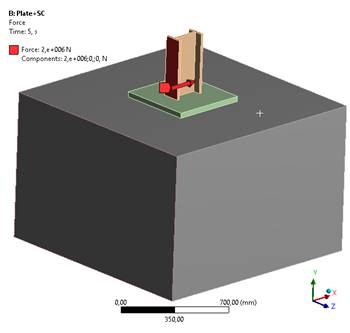
Figura 5. Cargas aplicadas – Fuerza dirección +X

Primero vamos a calcular de forma teórica, siguiendo la fórmula presentada de la ACI 318-19, cuánto cortante debería de resistir la llave de cortante y cuánto los pernos para este caso particular que estamos estudiando.

Para aplicar la fórmula definida arriba tenemos que definir Aef,sl, que según la ACI 318-19 se define como sigue:

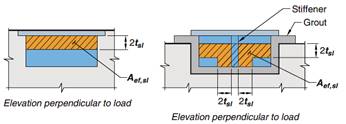
Figura 6. Aef,sl – ACI 318-19

Aplicando la imagen anterior, obtenemos un Aef,sl=6000mm² (que representa aproximadamente un 50% de la superficie de nuestra llave de cortante. Vamos a dar este valor por válido, pero más tarde lo vamos a comprobar. Lo aplicamos en la fórmula de la ACI 318-19 para obtener la relación Cortante por perno / Cortante total aplicado:

Vamos a comprobar este número teórico con lo que obtenemos cuando aplicamos la carga de cortante creciente en el modelo de elementos finitos que hemos presentado. La siguiente imagen nos muestra en función de la carga aplicada, qué cantidad de la misma se transmite al hormigón a través de la llave de cortante y que cantidad a través de los pernos:

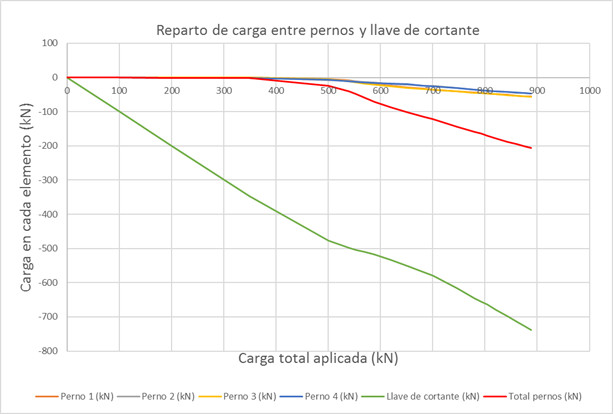
Figura 7. Reparto de carga entre pernos y llave de cortante

Vamos a traducir esto en %, es decir, que porcentaje de la carga se transmite por los pernos comparado con la carga total aplicada para poder compararla rápidamente con el valor de 6.4% obtenido anteriormente. La siguiente imagen nos muestra estos porcentajes:

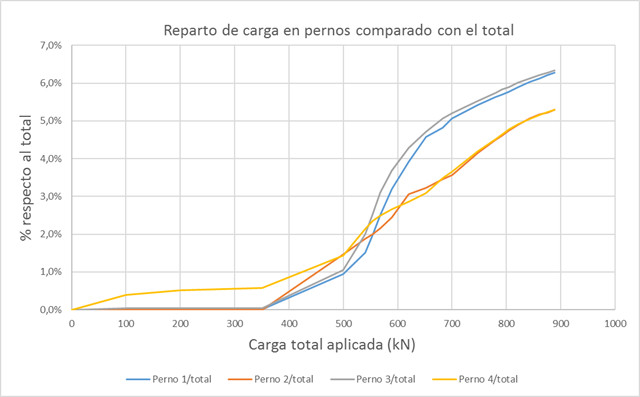
Figura 8. Porcentaje de carga en pernos comparado con la carga total

Vamos a analizar las imágenes presentadas arriba:

·         Hasta que no se alcanzan los 350kN de carga la llave de cortante resiste todo el cortante aplicado y los pernos prácticamente nada. Nota: el perno 4 parece resistir algo más inicialmente pero es producto de modelar pernos circulares con elementos finitos, se crean esquinas que ha hecho que el perno 4 entre en contacto unas micras de milímetro antes que el resto. Este es el momento, 350kN, en el que el hormigón comienza a plastificar. Recordamos que la resistencia del hormigón se podría aumentar mediante armados de confinamiento. Es a partir de este momento donde se empieza a producir un desplazamiento en la parte superior de la llave de cortante debido a la plastificación del hormigón. Al producirse este desplazamiento en esta zona hace que toda la placa tienda a desplazarse solidamente empezándose a apoyar en los pernos, a partir de aquí la carga en los pernos aumenta:

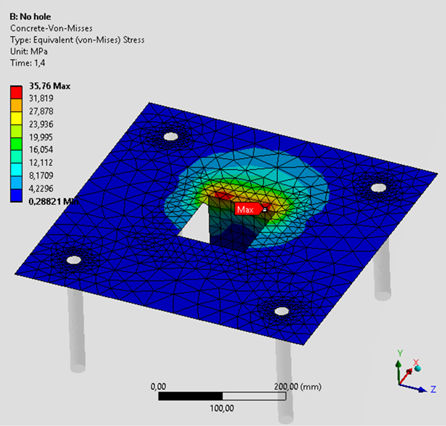
Figura 9. Estado de tensiones del hormigón para una carga aplicada de 350kN

·         Según va plastificando más el hormigón delante de la llave de cortante, más se van cargando los pernos. A partir de un cierto momento, 590kN, plastifica también el hormigón delante de los pernos, en este momento la velocidad a la que los pernos cogen cortante desciende un poco, pero siguen cogiendo carga a medida que aumentamos.

Figura 10. Estado de tensiones del hormigón para una carga aplicada de 590kN

·         Una vez plastificado el hormigón, cuando las cargas empiezan a ser elevadas, la participación de los pernos a la carga de cortante alcanza valores de 4% llegando hasta 6.3%. Este punto vamos a estudiarlo en detalle a continuación.

Vamos a estudiar la veracidad de la fórmula de la ACI 318-19. Según esta fórmula, el 6.4% de la carga de cortante total es resistida por cada perno y el resto es la llave de cortante quien la resiste. Como bien dice la ACI 318-19, este reparto se produce cuando empieza a existir un movimiento en el anclaje, ya que es este movimiento quien produce el reparto. Basándonos en los resultados, vemos que en los dos anclajes más solicitados, cuando alcanzamos carga elevadas, cerca de la rotura del sistema, llegamos a repartos del 6.0%-6.3% que es casi el valor exacto a lo que arroja el resultado de la ACI 318-19. Para valores más bajos de carga, habiendo alcanzado ya el estado de plastificación en varias zonas, tenemos repartos de 3%-5%. Alcanzamos una similitud muy alta entre la fórmula de la ACI 318-19 y nuestros cálculos.

Nos falta comprobar usando los resultados del cálculo del modelo, el área teórica usada, Aef,sl=6000mm², calculada basándonos en la ACI 318-19. La siguiente imagen muestra las zonas que superan los 10MPa. Nos hemos basado en este criterio para diseñar aproximadamente un área efectiva Aef,sl. Como vemos obtenemos 7151cm², que no está muy lejos del valor teórico propuesto por la ACI 318-19. Con este valor la fórmula anterior nos da 5.6%, que como vemos sigue siendo sobre el mismo orden de magnitud.

Figura 11. Aef,sl calculada con los resultados del modelo de elementos finitos

Las siguientes imágenes muestran la evolución de nuestro modelo según vamos aumentando las cargas:

Figura 12. Respuesta del modelo para distintas cargas – Desplazamiento en X (mm)

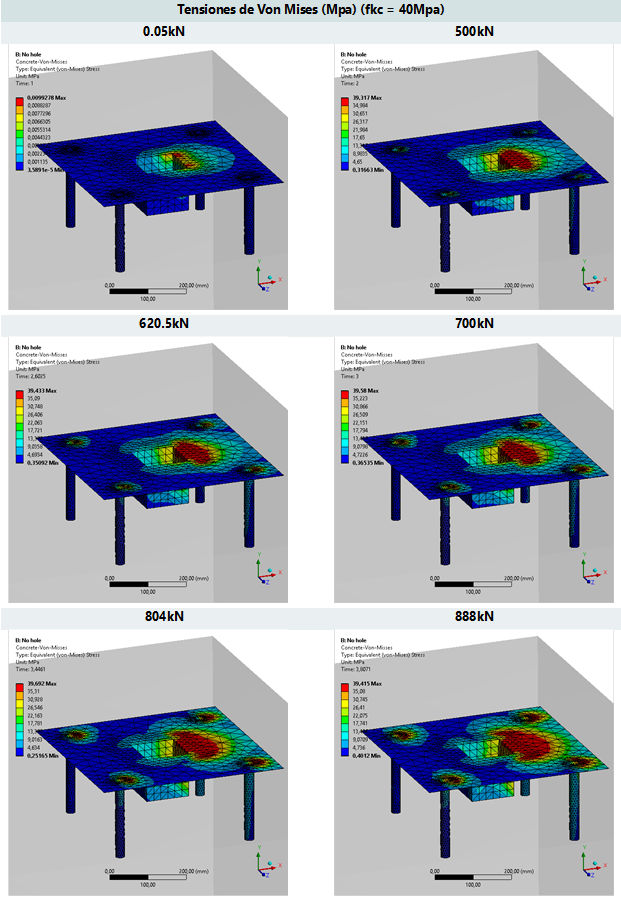
Figura 13. Respuesta del modelo para distintas cargas – estado de tensiones (MPa)

Conclusiones

·         La hipótesis de que la llave de cortante resiste todo el cortante sabemos que es falsa

·         El EC-2 no da mucha información al respecto. Sin embargo la ACI 318-19 en su apartado §17.11.1.1.3 nos dice como valorar la contribución de los pernos a la resistencia de cortante cuando tenemos llave de cortante

·         Nuestro cálculos demuestra que los valores propuestos por la ACI 318-19 son muy semejantes a los que obtenemos usando nuestro modelo de elementos finitos

·         El área efectiva que propone la ACI 318-19 (área de la llave de cortante en contacto con el hormigón bajo cargas de cortante) es bastante realista. Hay que decir que hemos tenido que hacer hipótesis para calcular nuestra área efectiva usando nuestro modelo de elementos finitos. Hemos considerado para este área solo aquellas zonas superiores a 10Mpa de compresión. Este ha sido un valor arbitrario, sin base teórica por detrás.